


Hydrodynamic performance of psammosteids: New insights from computational fluid dynamics simulations
MAREK DEC
The shape of dermal armor protecting the body in the Paleozoic agnathans such as the Heterostaci has an important hydrodynamic role in providing lift or drag force generation. Here, by performing computational fluid dynamics simulations (CFD), the measurements of hydrodynamic lift/drag force and lift or drag coefficients were taken for two psammosteids Guerichosteus and Tartuosteus with reference to the pteraspid Errivaspis. This study shows the substantially higher values of the lift coefficient and lift-to-drag ratio for the psammosteids Guerichosteus and Tartuosteus compared with Errivaspis. The tendencies in the evolution of dermal exoskeleton, especially the widening of the branchial plates of psammosteids was directed towards the increased generation of lift force to provide efficient cruising.
Introduction
The Heterostraci are a Silurian–Devonian clade of jawless vertebrates characterized by a pair of common external branchial openings. The two major groups are Cyathaspidiformes and Pteraspidiformes and are represented by a large variety of forms (e.g., Blieck 1984; Denison 1964; Janvier 1996). Cyathaspids posses a head shield that is oval to almost circular in cross section, an adaptation belived to be related to producing lift force for a rapid rise from the bottom (Novitskaya 2007). Pteraspis, in turn, also have oval cross-sections of a head shield but are wider laterally. Conversely, the head shield of psammosteids are dorso-ventral asymmetric with wide branchial plates (Obruchev and Mark-Kurik 1965; Tarlo 1964, 1965), which are purportedly more efficient at creating lift.
The fish body shape is significantly connected to functional aspects of hydrodynamic, locomotion, and their swimming mode (Aleyev 1977; Webb 1984). Therefore the study of these aspects on Recent fishes offers the tools for the partial reconstruction of the mode of life and habits of fossil fishes. Recently, the hydrodynamics of the cephalic shield of Errivaspis was studied in a wind tunnel to show the detailed flow pattern around the head shield which was shown to be comparable with a delta wing aircraft (Botella and Farina 2008).
The purpose of this article is to investigate the hydrodynamic effects of the psammosteid body plan, a poorly understood feature of psammosteid morphology. Psammosteids are considered to be bottom-dwellers (Tarlo 1957). Some authors suggested that they fed on starfish which they picked up from the sea floor (Patten 1932), but they have also been interpreted as mud grubbers living in shallow seas (Tarlo 1965). The wide and downwardly curved branchial plates of large psammosteids were considered to be a support while resting on soft bottom substrates (Janvier 1996). In addition to the supporting nature of the head shield, the tail fin of the psammosteid Drepanaspis gemuendenensis, which comprises the 1/4 of the total length of the body, is responsible for generating considerable propulsive force (Mark-Kurik 1992). These fishes, regardless of their possible substrate-dwelling habits, were also capable of active swimming.
A new reconstruction of Guerichosteus kozlowskii recently shed light on the body shape of this psammosteids (Dec 2019). The development of computer methods that use numerical analysis and data structures to solve and analyze problems that involve fluid flows (computational fluid mechanics) gives the possibility of a better understanding of the hydrodynamic properties (Rahman 2017) of the psammosteid body form.
Assessing the drag and lift forces, generated on hydrofoils is an important step in identifying the performance characteristic of the hydrofoil during swimming. This study focusses on the psammosteid gliding locomotion, especially the influence of the geometrical shape of the psammosteid body form on hydrodynamic performance. In this instance, gliding involves the motionless movement of the body through a current and represents the steady state condition of flow over the body surface.
Abbreviations.—A, surface wetted area [m2]; α, angle of attack; CD, drag coefficient; CL, lift coefficient; CL/CD, lift-to-drag ratio; CFD, computational fluid dynamics; D, drag forces [N]; L, lift forces [N]; N, Newtons; p, pressure [Pa]; ρ, density of fluid; Re, Reynolds number; U, velocity [ms-1]; v, kinematic viscosity [m2s-1].
Methods
The computer used for the simulation is a Linux Ubuntu 18.10 machine running on a Intel® Core™ i7-2630QM CPU 2.00GHz × 8 with 16GB RAM.
Mesh generation.—A 3D model of Errivaspis and Guerichosteus (Fig. 1) was created using the free and open-source 3D computer graphics software Blender. The model of Errivaspis was created based on Botella and Farina (2008). Only the tail was modified where the extended lower lobe was shortened (Mark-Kurik and Botella 2009). The Guerichosteus mesh was created in reference to work by Dec (2019) concerning the revision and 3D reconstruction of the genus. To compare the geometry characteristics of the 3D models, all models were scaled to the same length (0.5 m). The triangulated surface geometries were exported from Blender as .stl files to the snappyHexMesh tool (OpenFoam). A computational box-shaped flow domain with width and height of 2 m and a length of 3 m was generated (Fig. 1A1) (Moukalled et al. 2016). To increase mesh fineness around the fish models a refinement volume region (1.18 m in length, 0.38 m in width and height) was set. The cells (with additional cells layer near surface) are mostly located in the region around the model which allows for a good resolution of the wake region (Moukalled et al. 2016). The mesh statistics are shown in Table 1 and details of the grid generated around the model are shown in Fig. 1A2.
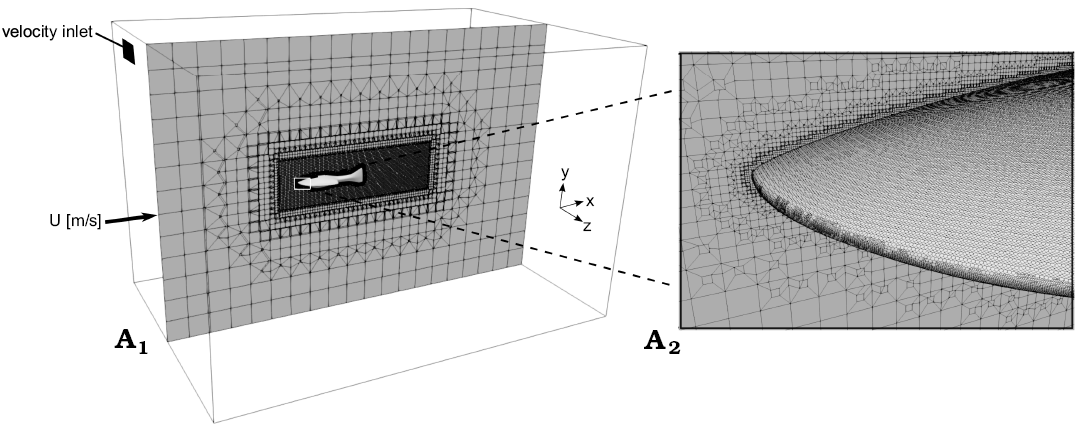
Fig. 1. Box-shaped flow domain, mesh and coordinate system used for computational fluid dynamics (A1); A2, enlargement view on the mesh.
Table 1. The mesh statistics.
| |
Errivaspis |
Guerichostes |
Tartuosteus |
|
Area [m2] |
0.100157 |
0.158854 |
0.192262 |
|
Number of cells |
1 549 095 |
2 351 444 |
2 871 719 |
|
Number of surface cells |
277 381 |
449 677 |
524 244 |
|
Average surface face area [m2] |
3.61e-07 |
3.53e-07 |
3.67e-07 |
|
Minimum surface face area [m2] |
2.34e-09 |
2.65e-09 |
1.28e-09 |
Boundary and initial condition.—The range of Reynolds numbers conducted in simulation varies from 238 000 to 1 190 000, using the equation Re = Ul/v, where U is the flow speed (ms-1), l is the length of the object in the direction of flow, in this case the chord length (0.5 m), v refers to the kinematic viscosity (sea water = 1.05e-6 m2s-1). The simulation consists of flow around a fish model at various angles of attack (α) and velocity. The angle of attack converging a range from -10 to +20 degrees in two degree increments.
The boundary face was defined as the velocity inlet with various speed (0.5 ms-1, 1.5 ms-1, 2.5 ms-1) in different cases. In analogy to the previous analysis of Errivaspis the swimming speed was estimated for three body length per second (Botella and Farina 2008). Here for the model of 0.5 m long, the swimming speed of three body length per second gives the value of velocity 1.5 ms-1. The top speed of five body length per second (here 2.5 ms-1) is applied in reference to the boxfish (Van Wassenbergh et al. 2014). This fish has a carapace protecting the body so undulation to power swimming is limited to rare. Therefore, like psammosetids are believed to have swum, the acceleration is a result of the single beats of the caudal fin.
The front, back, upper and lower walls were set to slip boundary condition to provide a slip constraint. For the simulation of turbulent flows the Reynolds-Averaged Simulation (RAS) model was applied with komegaSST turbulent modeling. The simpleFoam steady-state solver for incompressible, turbulent flow was used in the open-source package OpenFoam. This solver uses the SIMPLE algorithm which is an iterative process that is repeated until convergence. In most cases iterative convergence was reached after 500 iterations. The simulation result is the sum of the forces acting in each direction on the model, or any part of it. The lift and drag force were calculated in Paraview software by summing up the pressure distribution around the whole model surface.
Lift force is defined as the component of the net force (due to viscous and pressure forces) that is perpendicular (along Y axis) to the flow direction (along X axis). Drag force is the component of the net force along the flow direction (along X axis), that is opposed to the motion. So the lift and drag force of the model is the vector sum of the pressure times the area around the entire solid body.
The lift or drag coefficient has been applied to eliminate the size effect as a universally comparable measure of lift/drag force. The lift and drag coefficient is a number used to model all of the complex dependencies of shape (size and body shape), inclination, and some flow conditions (velocity, viscosity).
The lift coefficient CL = 2L/ρU2A.
The drag coefficient CD = 2D/ρU2A.
Results
Pressure.—The surface pressure distribution on the fish models at 1.5 ms-1 velocity is presented on Fig. 2. Defined gauge pressure is the pressure relative to 0 Pa set in simulation boundary condition. Gauge pressure is positive for pressures above boundary condition pressure, and negative for pressures below it.
In each models, the highest pressures are registered in the anterior part of the head and at the leading edges of the branchial plates in the case of Tartuosteus. The lowest pressures are observed in the middle and thickest part of the head shield. The area of low pressure extends around the mid part of the body, including branchial plates, of Tartusteus. While in Guerichosteus and Errivaspis it is mainly observed in the ventral plate.
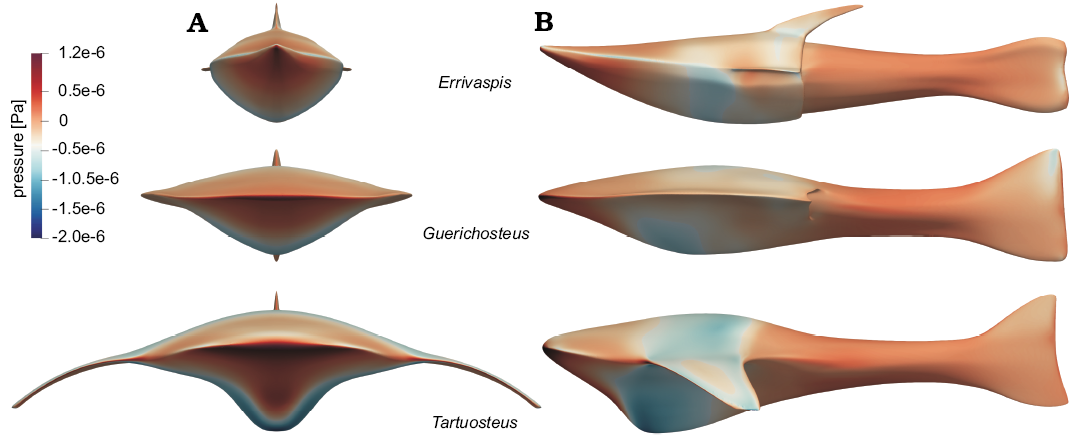
Fig. 2. Distribution of pressure on the fish bodies at flow velocity 1.5 ms-1, in anterior (A1) and lateral (A2) views.
Lift.—The variation of lift coefficient with angle of attack and various flow speeds are shown in Fig. 3A. The lift coefficient increases near linearly with the angle of attack α for each tested flow velocity for all three models. Only for Tartuosteus CL reaches a maximum at about 8°, and then starts to decrease. This decrease of lift is called stall and it is generated by flow separation. It is not observed for two other models due to a limited range of analysis and it will occur at high angles of attack.
Drag.—The most efficient model for generating lift, indicated by body orientation, also exhibits the lowest drag (Fig. 3B). The lowest drag observed in all three genera is between -4° and 0° α for 0.5 ms-1 and 1.5 ms-1 velocity and rapidly increased with increasing angle of attack. At a velocity of 2.5 ms-1 the drag coefficient CD shows a similar pattern to the drag force for Errivaspis, whereas for Guerichosteus (α -6° to -4°) and Tartuosteus (α -4° to -2°) a narrower range of degree of the lowest CD was found than in Errivaspis.
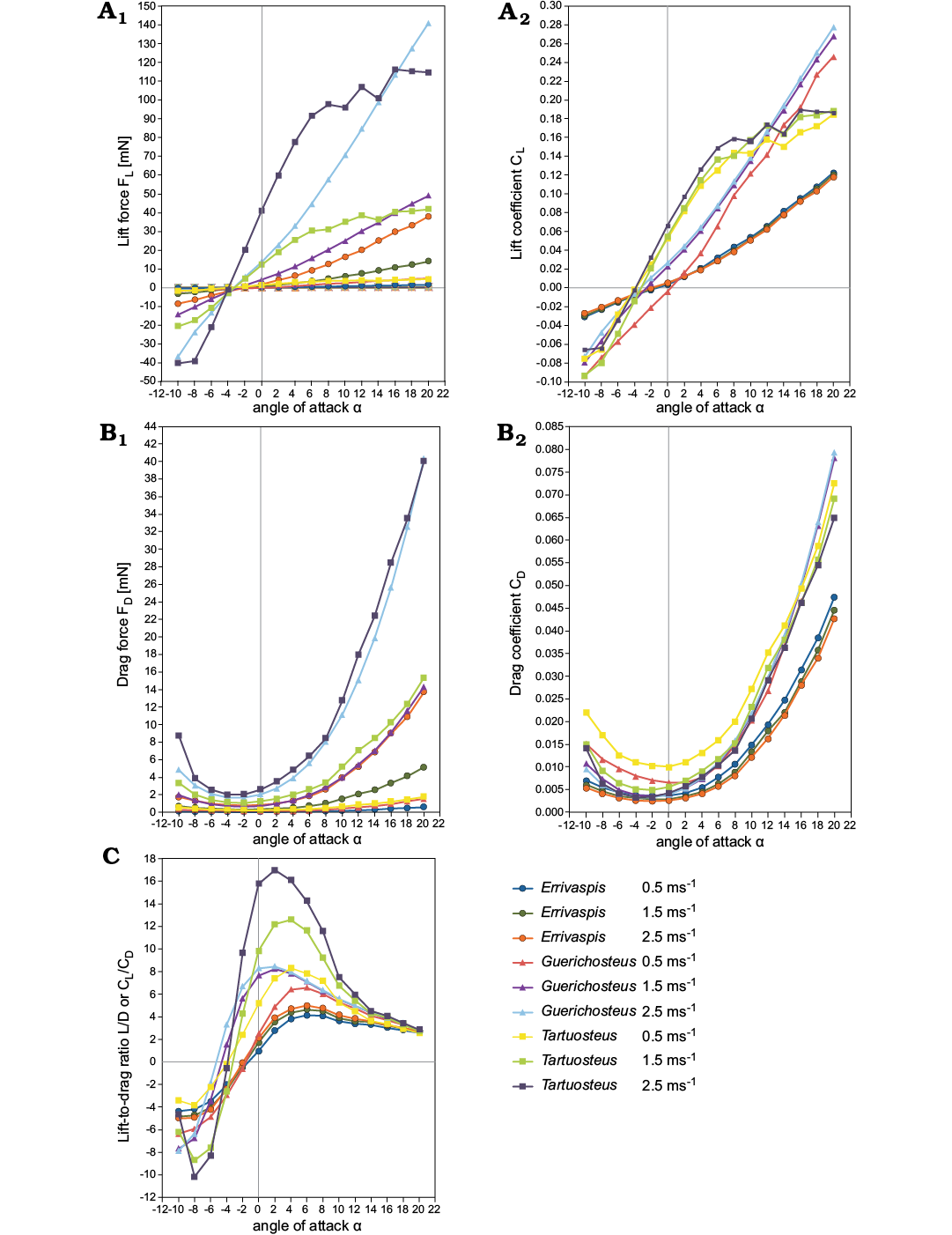
Fig. 3. Comparison lift (A), drag (B), lift-to-drag ratio (C) versus the angle of attack at various velocity for Errivaspis, Guerichosteus, and Tartuosteus.
The minimum drag coefficient at 0.5 ms-1 flow velocity for the three genera can be ordered as: Errivaspis (CD = 0.0037) < Guerichosteus (CD = 0.0065) < Tartuosteus (CD = 0.0101). In all models the drag coefficient decreased with increasing velocity. So when flow velocities increased to 2.5 ms-1, the minimum CD for Errivaspis decreased as well (CD = 0.0025). This value is smaller than for the other two genera Guerichosteus and Tartuosteus, where drag coefficient values are almost the same (CD = 0.0033) at 2.5 ms-1.
The tip vortex associated with induced drag is generated by the branchial plate tip, similar to an airplane wing (see Çengel and Cimbala 2006: fig. 10-49, 10-50). The produced vortices reduce the pressure along the rear edge of the branchial plate, increasing drag. The vorticity shown in Fig. 4 is presented with the iso-vorticity surface at U = 1.5 ms-1 and α = 0° and identified by Q-criterion (Kolář 2007). The most abundant vortex is observed in Tartuosteus and Guerichosteus, and is considerably less in Errivaspis. However, through analogy from modern aircraft, the further a trailing vortex is from the body of the branchial plates, the less influence on the plate (Çengel and Cimbala 2006). Therefore Tartuosteus long branchial plates produce less drag produced by vortex drag than Guerichosteus, but reduce maneuverability because of their larger moment of inertia.
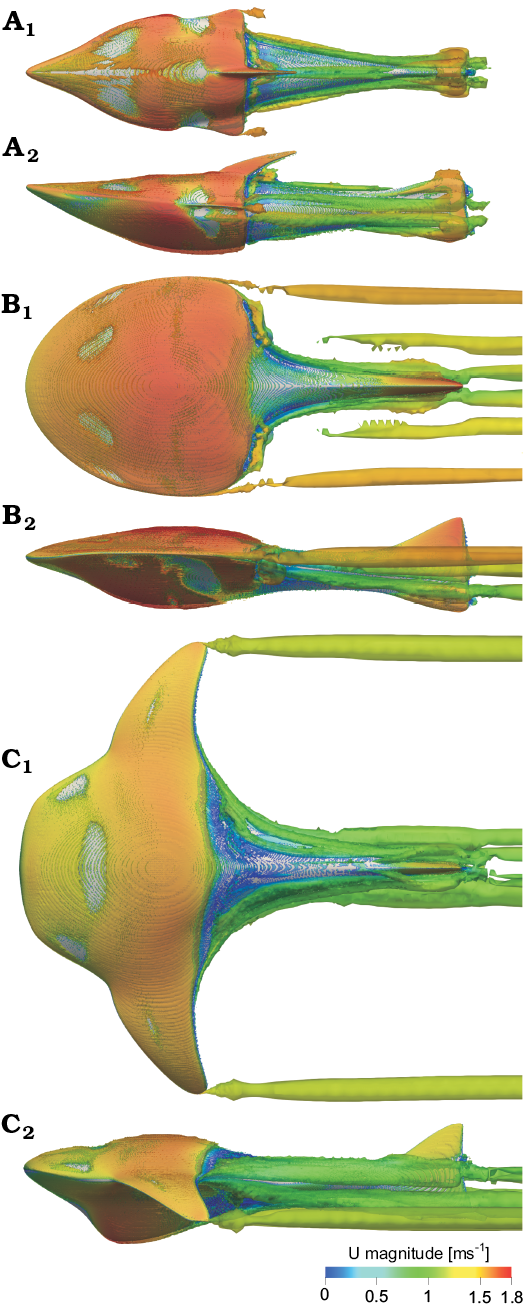
Fig. 4. Vorticity patterns using Q-criterion for 0 angles of attack and flow velocity 1.5 ms-1 in Errivaspis (A), Guerichosteus (B), and Tartuosteus (C). Models displayed in left lateral (A1–C1) and top (A2–C2) views. Iso-vorticity surface is colored by the magnitude of velocity.
Lift-to-drag ratio.—The ratio is a measure of hydrodynamic performance for the fish model, which is equivalent to the ratio of the lift-to-drag coefficients CL/CD. This is shown in Fig. 3C in a plot of CL/CD versus the angle of attack with various speed (0.5 ms-1, 1.5 ms-1, 2.5 ms-1).
The lift-to-drag ratio of three genera increases with the angle of attack α. At a velocityof 0.5 ms-1 it reaches a maximum at α = 4° for Tartuosteus, α = 6° for Errivaspis and Guerichosteus. For the three genera, the maximum CL/CD of 0.5 ms-1 flow velocity is ordered: Errivaspis (CL/CD = 4.13) < Guerichosteus (CL/CD = 6.56) < Tartuosteus (CL/CD = 8.29). In a higher flow velocity of 2.5 ms-1 the lift-to-drag ratio differs from the lower velocities and the maximum CL/CD is at α = 2° for Tartuosteus and Guerichosteus and α = 6° for Errivaspis. In Tartuosteus the lift-to-drag ratio at 2.5 ms-1 flow velocity increased twice to 16.99 compared to 0.5 ms-1, while for Errivaspis it raised only to 4.98 and for Guerichosteus to 8.46.
Concluding remarks
CFD simulation was performed to investigate the hydrodynamic properties (qualitative and quantitative) of gliding psammosteids, Guerichosteus (Early Devonian) and Tartuosteus (Middle Devonian). The properties of their body armor differ mostly in the proportions of the branchial plates, which are broader in Tartuosteus (Obruchev and Mark-Kurik 1965) than in Guerichosteus (Dec 2019), and is critical for hydrodynamic efficiency, where the main propulsive power is generated by the tail. CFD simulation of the three agnathan genera has been performed to verify the hypothesis that the broadening of the branchial plate increased the lift force generation to provide efficient cruising.
Changing the angle of attack has been shown to result in a change of lift and drag. The more streamlined body produces a lower drag coefficient, and for the three genera studied, Errivaspis has the lowest drag coefficients at varying current velocities followed Guerichosteus then Tartuosteus. The drag coefficient is comparable to living animals, for example dolphins, in which the drag coefficient on the wetted skin area is about 0.0035 (Çengel and Cimbala 2006). Producing the least drag and generating the most lift are desirable characteristics of swimming organisms that need to maintain a depth in the water column. The change of the lift and drag characteristics of models is related to the changes of the angles of attack. The most favorable lift-to drag ratio (positive values) at higher velocities of 2.5 ms-1 was experienced by Tartuosteus. Guerichosteus and Errivaspis exhibited similar lift-to drag ratios at the same velocity. To produce more lift, the angle of attack has to be higher, however, the maximum CL/CD is noted in lower angles of attack for Tartuostaus and Guerichosteus than for Errivaspis. The highest lift-to-drag ratio is noted for Tartuosteus (CL/CD = 16.99) which is comparable to jet airplane (Airbus A320-200 CL/CD = 16.3; Martinez-Val et al. 2005).
This study demonstrates the adaptive reason behind the relative widening of branchial plates in psammosteids. The widening of branchial plates increases the lift force, which apparently provide efficient cruising. Additionally, the wider branchial plates of Tartuosteus might have reduced its maneuverability, comparing to Guerichosteus and Errivaspis.
Higher hydrodynamic quality suggests advantages of Tartuosteus in more effective acquisition of widely distributed food or for predator escape. However, the ecomorphologic classification is still ambiguous, there is not enough information of the ecological connection of psammosteids with the bottom (benthonekton) or with the water column (planktonekton, eunekton).
Acknowledgements.—I thank Przemysław Gorzelak (Institue of Paleobiology, PAS, Warsaw, Poland) for a fruitful discussions on hydrodynamic and correction on drafts of this manuscript. I would especially like to thank Héctor Botella (University of Valencia, Spain) and Tom Challands (University of Edinburgh, UK) for their constructive reviews of the manuscript.
References
Aleyev, Y.G. 1977. Nekton. vi + 435 pp. Dr. W. Junk, The Hague. Crossref
Blieck, A. 1984. Les Hétérostracés Ptéraspidiformes, Agnathes du Silurien–Dévonien du Continent nord-atlantique et des blocs avoisinants: révision systématique, phylogénie, biostratigraphie, biogéographie. Cahiers de Paléontologie 6. 202 pp. Muséum national d’Histoire naturelle, Paris.
Botella, H. and Fariña, R.A. 2008. Flow pattern around the rigid cephalic shield of the devonian agnathan Errivaspis waynensis (Pteraspidiformes: Heterostraci). Palaeontology 51: 1141–1150. Crossref
Dec, M. 2019. Revision of the Early Devonian psammosteids from the “Placoderm Sandstone” implications for their body shape reconstruction. Palaeontologia Electronica 22.2.36A [published online] Crossref
Çengel, Y.A. and Cimbala, J.M. 2006. Fluid Mechanics: Fundamentals and Applications. 992 pp. McGraw-Hill Higher Education, Boston.
Denison, R.H. 1964. The Cyathaspididae: a family of Silurian and Devonian jawless vertebrates. Fieldiana Geology 13: 30–473. Crossref
Janvier, P. 1996. Early Vertebrates. 393 pp. Oxford Science Publications, Clarendon Press, Oxford.
Kolář, V. 2007. Vortex identification: New requirements and limitations. International Journal of Heat and Fluid Flow 28: 638–652. Crossref
Mark-Kurik, E. 1992. Functional aspects of the armour in the early vertebrates. In: E. Mark-Kurik (ed.), Fossil Fishes as Living Animals, 107–116. Academia, Tallinn.
Mark-Kurik, E. and Botella, H. 2009. On the tail of Errivaspis and the condition of the caudal fin in heterostracans. Acta Zoologica 90: 44–51. Crossref
Martinez-Val, R., Perez, E., and Palacin, J.F. 2005. Historical evolution of air transport productivity and efficiency. AIAA 2005-121. In: 43rd AIAA Aerospace Sciences Meeting and Exhibit. American Institute of Aeronautical and Astronautics, Reno, Nevada. Crossref
Moukalled, F., Mangani, L., and Darwish, M. 2016. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab. T. 113. Fluid Mechanics and Its Applications. 777 pp. Springer International Publishing, Cham. Crossref
Novitskaya, L.I. 2007. Evolution of generic and species diversity in Agnathans (Heterostraci: orders Cyathaspidiformes, Pteraspidiformes). Paleontological Journal 41: 268–280. Crossref
Obruchev, D. and Mark-Kurik, E. 1965. Psammosteidy (Agnatha, Psammosteidae) devona SSSR. 304 pp. Institute of Geology, Academy of Sciences of the Estonian SSR, Tallinn.
Patten, W. 1932. Foundation of the face. Scientific Monthly 35: 511–521.
Rahman, I.A. 2017. Computational Fluid Dynamics as a tool for testing functional and ecological hypotheses in fossil taxa. Palaeontology 60: 451–59. Crossref
Tarlo, L.B. 1957. A preliminary note on new ostracoderms from the Lower Devonian (Emsian) of central Poland. Acta Palaeontologica Polonica 2: 225–233.
Tarlo, L.B. 1964. Psammosteiformes (Agnatha)—a review with descriptions of new material from the Lower Devonian of Poland. Part I. Palaeontologia Polonica 13: 1–135.
Tarlo, L.B. 1965. Psammosteiformes (Agnatha)—a review with descriptions of new material from the Lower Devonian of Poland. Part II. Palaeontologia Polonica 15: 1–168.
Webb, P.W. 1984. Body form, locomotion and foraging in aquatic vertebrates. American Zoologist 24: 107–120. Crossref
Van Wassenbergh, S., van Manen, K., Marcroft, T.A., Alfaro, M.E., and Stamhuis, E.J. 2014. Boxfish swimming paradox resolved: forces by the flow of water around the body promote manoeuvrability. Journal of The Royal Society Interface 12: 20141146 [published online]. Crossref
Marek Dec [mdec@wp.pl], Institute of Palaeobiology, Polish Academy of Sciences, Twarda 51/55, 00-818 Warszawa, Poland.
Received 15 April 2019, accepted 29 July 2019, 17 October 2019 available online.
Copyright © 2019 M. Dec. This is an open-access article distributed under the terms of the Creative Commons Attribution License (for details please see http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Acta Palaeontol. Pol. 64 (4): 679–684, 2019
https://doi.org/10.4202/app.00623.2019